Random Variables

What is a Random Variable?

The term itself can be misleading (random variable is neither random nor a variable). It is actually a function or mapping which takes all the elements from a sample space and maps them to real numbers.

For example, let’s take our random experiment to be tossing a coin once. The sample space contains only two possible outcomes, heads (H) and tails (T). We assign a value of 1 to the outcome H, and an outcome 0 to the outcome T. So X(H) = 1, X(T) = 0.

Visually we can think of something like this:

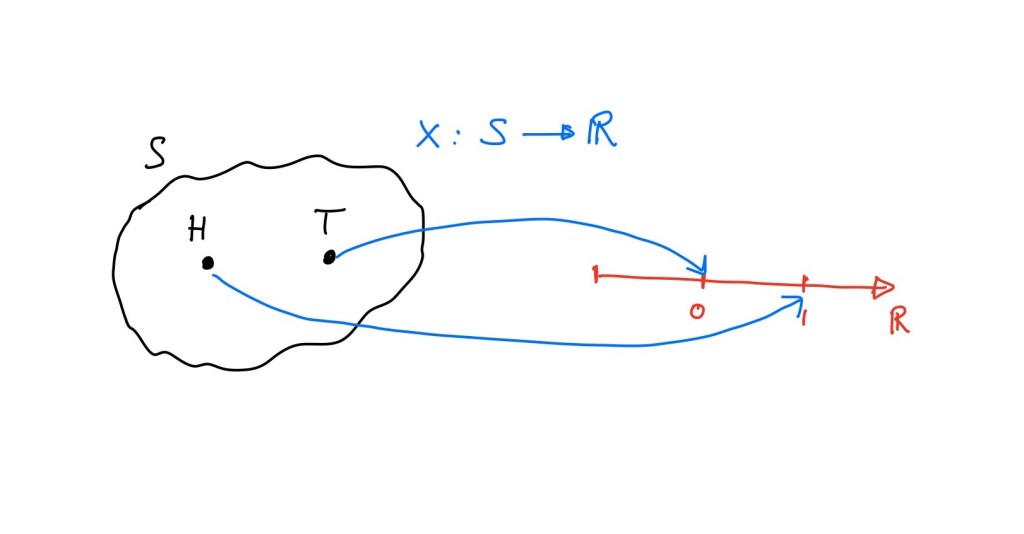
But we can chose the values (1,0) to be anything we like….they could be -50 and +100, for example.

If we consider the experiment to be tossing a fair coin twice, the sample space will contain four possible outcomes – HH, HT, TT, TH. We could define our random variable to be the total number of heads (X), or the number of heads on the first toss (Y). So we can see that for the same sample space of experiment, we can have multiple random variables, some will be more natural than others.

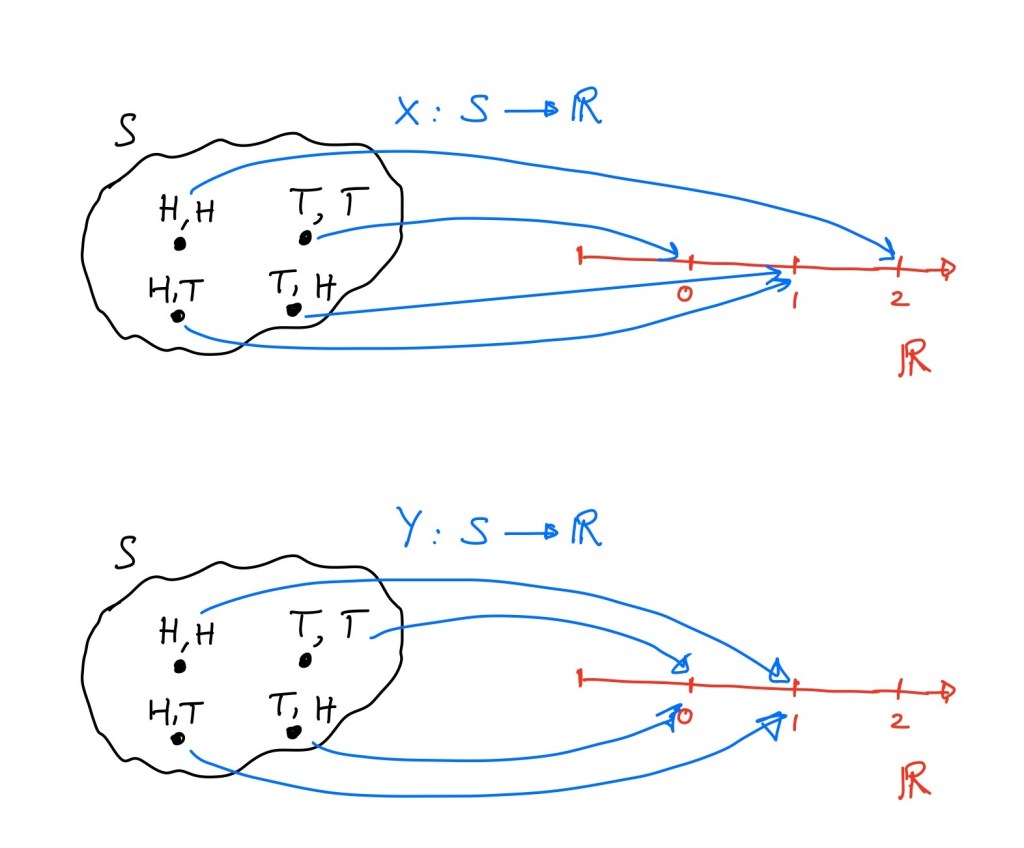
Continuous/Discrete Random Variables

If the random variable has a countable number of possible values, then it is a discrete (value) random variable.

If the random variable take all possible values in a given interval (think of a range of values on the real line), then it is a continuous (value) random variable. Simple examples are things like height, weight, time.